Introduction
In today's data-driven world, making informed decisions about product changes is crucial. A/B testing offers a powerful framework for gathering actionable insights and making evidence-based decisions, particularly in web and app development. In this blog post, we delve into the essential principles of designing, executing, and analyzing an A/B test using a practical, real-world example.
The Experimental Context: A Widget Store's Coupon Code Dilemma
Our example centers on a fictional online commerce platform specializing in selling widgets. In an effort to boost sales, the marketing team proposes a strategy involving promotional emails that include a coupon code for discounts on widgets. This proposal marks a potential shift in the company's business model, as they have never offered coupon codes before. The team is cautious, however, due to findings from prior studies—such as Dr. Footcare's revenue loss following the introduction of coupon codes (Kohavi, Longbottom et al., 2009) and evidence from GoodUI.org suggesting that removing coupon codes can be beneficial (Linowski, 2018). These insights raise concerns that simply adding a coupon code field to the checkout page might negatively impact revenue, even if no valid codes are available. Users might become distracted searching for codes or even abandon their purchases altogether.
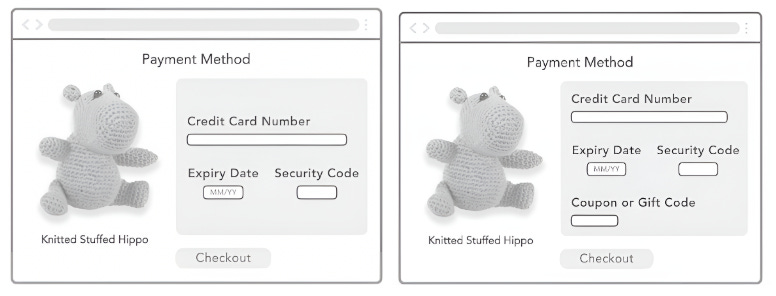
To assess these potential effects, we adopt a “painted door” approach. This involves implementing a superficial change—adding a non-functional coupon code field to the checkout page. When users input any code, the system responds with “Invalid Coupon Code.” By focusing on this minimal implementation, we aim to evaluate the psychological and behavioral impact of merely displaying a coupon code field.
Given the simplicity of this change, we’ll test two distinct UI designs to compare their effectiveness. Testing multiple treatments alongside a control allows us to discern not only whether the idea of adding a coupon code is viable, but also which specific implementation is most effective. This targeted A/B test is a crucial step toward determining the feasibility of adopting coupon codes as part of the company’s broader business strategy.
Hypothesis
Adding a coupon code field to the checkout page will degrade revenue-per-user for users who start the purchase process.
To test this hypothesis, we consider two UI implementations. This A/B test is a critical step in assessing the feasibility of this business model.
Goal Metrics
The primary metric, or Overall Evaluation Criterion (OEC), is revenue-per-user, normalized to account for sample size variability. To measure the impact of the change, we define success metrics carefully. While revenue is an obvious choice, using the total revenue sum is not recommended due to sample size variations across variants. Instead, revenue-per-user provides a more accurate and normalized metric. For this metric, it is critical to determine the denominator:
Including all site visitors introduces significant noise, as a large portion of users never initiate checkout. These users do not interact with the modified checkout process and, therefore, cannot provide meaningful data on the impact of the change. Including them dilutes the results, making it harder to detect any real differences caused by the experiment.
Restricting to only users who complete the purchase process presents a skewed perspective, as it inherently assumes that the modification influences purchase amounts without considering its effect on conversion rates. This approach excludes users who might abandon the process due to the change, potentially missing a critical aspect of the experiment's impact.
The best choice is users who start the purchase process, as they are directly exposed to the change at the checkout stage. This refined approach improves test sensitivity by ensuring that only the users who interact with the modified UI are analyzed. By excluding unaffected users, such as those who browse without adding items to the cart or initiating a purchase, the metric becomes more precise. This specificity helps isolate the true impact of the coupon code field, avoiding noise introduced by broader user behaviors that are irrelevant to the experiment.
With this setup, our refined hypothesis becomes: “Adding a coupon code field to the checkout page will degrade revenue-per-user for users who start the purchase process.”
Hypothesis Testing
Before we can design, run, or analyze our experiment, let us go over a few foundational concepts relating to statistical hypothesis testing. First, we characterize the metric by understanding the baseline mean value—the average of the metric under normal, unaltered conditions—and the standard error of the mean. The standard error provides insight into the variability of our metric estimates and is crucial for determining the required sample size to detect meaningful differences. By accurately estimating this variability, we can size our experiment properly and assess statistical significance during analysis.
For most metrics, we measure the mean, but alternative summary statistics, such as medians or percentiles, may be more appropriate in specific contexts, such as highly skewed data distributions. Sensitivity, or the ability to detect statistically significant differences, improves when the standard error of the mean is reduced. This can be achieved by either increasing the traffic allocated to the experimental variants or running the experiment for an extended period. However, running longer experiments may yield diminishing returns after a few weeks due to sub-linear growth in unique users (caused by repeat visitors) and potential increases in variance for certain metrics over time.
To evaluate the impact of the experiment, we analyze revenue-per-user estimates from the Control and Treatment samples by computing the p-value for their difference. The p-value represents the probability of observing the measured difference, or a more extreme one, under the assumption that the Null hypothesis—that there is no true difference—is correct. A sufficiently small p-value allows us to reject the Null hypothesis and infer that the observed effect is statistically significant. But what constitutes a small enough p-value?
Typically, the scientific benchmark is a p-value less than 0.05. This threshold means there is less than a 5% probability of incorrectly concluding there is an effect when none actually exists, providing confidence in 95 out of 100 cases. Furthermore, another approach to determine significance is through confidence intervals. A 95% confidence interval defines a range where the true difference between Treatment and Control lies 95% of the time. If this interval does not include zero, it reinforces the conclusion that the effect is statistically significant. These tools collectively help establish the robustness of experimental findings, ensuring decisions are data-driven and reliable.
Statistical Power
Statistical power measures the ability of an experiment to detect a meaningful difference between variants when such a difference truly exists. In simple terms, it is the probability of correctly rejecting the null hypothesis when there is an actual effect. For instance, if a retailer is testing a new homepage layout, statistical power ensures that subtle but real increases in sales do not go unnoticed.
To achieve reliable results, experiments are often designed with 80-90% power, meaning there is a high likelihood of detecting true changes. Power is influenced by factors such as sample size and effect size; larger sample sizes tend to improve power, but overly small differences might still evade detection. For example, while a large e-commerce platform like Amazon might be interested in detecting a 0.2% increase in revenue-per-user due to its massive scale, a smaller startup might focus only on changes exceeding 5-10% because such increases are critical for their growth.
While statistical significance helps us understand whether an observed difference is likely due to chance, it does not always translate into practical significance. Practical significance asks a more business-oriented question: Is the observed change large enough to matter? For example, a 0.2% increase in revenue-per-user might be meaningful for billion-dollar platforms like Google or Bing, but for a small startup seeking rapid growth, a 2% increase might still fall short of expectations. Setting clear business thresholds for what constitutes a meaningful change is essential. For our hypothetical widget store, we define practical significance as a 1% or larger increase in revenue-per-user, recognising this as the minimum impact needed to justify potential costs or risks of implementation.
Designing the Experiment
We are now ready to design our experiment. We have a hypothesis, a practical significance boundary, and we have characterised our metric. We will use this set of decisions to finalize the design:
What is the randomisation unit? The randomisation unit for this experiment is the user.
What population of randomisation units do we want to target? We will target all users and analyse those who visit the checkout page. Targeting a specific population allows for more focused results. For instance, if the new text in a feature is only available in certain languages, you would target users with those specific interface locales. Similarly, attributes such as geographic region, platform, and device type can guide targeting.
How large does our experiment need to be? The experiment size directly impacts the precision of results. To detect a 1% change in revenue-per-user with 80% power, we will conduct a power analysis to determine the sample size. The following considerations influence size:
Using a binary metric like purchase indicator (yes/no) instead of revenue-per-user can reduce variability, allowing for a smaller sample size.
Increasing the practical significance threshold—for example, detecting only changes larger than 1%—can also reduce sample size requirements.
Lowering the p-value threshold, such as from 0.05 to 0.01, increases sample size needs.
How long should the experiment run? To ensure robust results, we will run the experiment for at least one week to capture weekly cycles and account for day-of-week effects. External factors like seasonality and primacy or novelty effects are also important:
User behavior can vary during holidays or promotional periods, affecting external validity.
Novelty effects (e.g., initial enthusiasm for a new feature) and adoption effects (e.g., gradual user adoption) may impact results over time.
Final Experiment Design
Randomization Unit: User
Target Population: All users visiting the checkout page
Experiment Size: Determined via power analysis to achieve 80% power for detecting a 1% change
Experiment Duration: Minimum of one week to capture weekly cycles and extended if novelty or primacy effects are detected
Traffic Split: 34/33/33% for Control, Treatment 1, and Treatment 2
By carefully designing the experiment with these considerations, we can ensure that the results are both statistically and practically significant. Overpowering an experiment is often beneficial, as it allows for detailed segment analysis (e.g., by geographic region or platform). This approach not only improves the robustness of results but also helps businesses uncover nuanced insights. For example, identifying specific trends in user behavior across different demographics can inform future product iterations and marketing strategies.
Furthermore, running a well-structured A/B test fosters a culture of data-driven decision-making within the organization. By investing in comprehensive experiment design and analysis, businesses can mitigate risks, allocate resources effectively, and achieve sustainable growth. Ultimately, the insights derived from this experiment will not only validate the feasibility of introducing coupon codes but also set a benchmark for future experimentation, reinforcing the importance of innovation and customer-centric strategies in a competitive market.
Running the Experiment and Getting Data
Now let us run the experiment and gather the necessary data. To run an experiment, we need both:
Instrumentation to get logs data on how users are interacting with your site and which experiments those interactions belong to.
Infrastructure to be able to run an experiment, ranging from experiment configuration to variant assignment.
Interpreting the Results
The data collected from the experiment is the foundation for actionable insights, but ensuring its reliability is critical. Before diving into the revenue-per-user analysis, it is essential to validate the experiment's execution by examining invariant metrics, also known as guardrail metrics. These metrics serve two primary purposes:
Trust-related Guardrails: Metrics such as sample size consistency and cache-hit rates ensure that the Control and Treatment groups align with the experiment configuration. Any deviation here might indicate issues in randomization or assignment.
Organizational Guardrails: Metrics like latency or system performance, which are crucial to business operations, should remain stable across variants. For example, significant changes in checkout latency would signal underlying problems unrelated to the coupon code test.
If these metrics show unexpected changes, it suggests flaws in the experiment design, infrastructure, or data processing pipeline. Addressing these issues before analyzing the core results is vital to maintaining trust in the findings.
Once the guardrails are validated, the next step is to analyze and interpret the results with precision. For example, if the p-value for revenue-per-user in both Treatment groups is below 0.05, we reject the null hypothesis and conclude that the observed differences are statistically significant. However, statistical significance alone is insufficient. Practical significance—the magnitude of the observed effect—determines whether the change is worth implementing.
Results Table
From the table, we observe that both treatments significantly reduce revenue-per-user compared to the control group. While the p-values confirm statistical significance, the negative impact on revenue highlights the need to reassess introducing coupon codes.
Decision-Making Framework
Consider the context of your experiment:
Short-Term vs. Long-Term Impact: Changes with minimal downside risks, such as testing promotional headlines, may allow for lower thresholds of significance. Conversely, introducing high-cost features like a coupon code system requires higher thresholds due to long-term resource commitments.
Balancing Metrics: A decrease in revenue may be acceptable if offset by an increase in user engagement, but only if the net impact aligns with organizational goals.
Ultimately, the results must translate into a clear decision framework. For example:
If the results are both statistically and practically significant, the decision to launch is straightforward.
If statistically significant but not practically meaningful, the change may not justify further investment.
If results are inconclusive, consider increasing sample size or re-evaluating the design.
The result is statistically significant, and likely practically significant. Like prior examples, it is possible that the change is not practically significant. In this situation, repeating the test with greater power is advisable. However, from a launch/no-launch perspective, choosing to launch is a reasonable decision. It is crucial to explicitly document the factors influencing this decision, particularly how they align with the practical and statistical significance boundaries. This clarity not only supports current decision-making but also establishes a solid foundation for future analyses.
By grounding decision-making in robust analysis and broader business considerations, organizations can confidently use A/B testing as a tool for sustainable growth and innovation.